【人工智能】Alpha-Beta剪枝算法

来源：www.45fan.com 2019-03-30 18:34:58

前言：在设计一款棋类博弈游戏的APP时，用到了Alpha-Beta剪枝算法，当时查尽资料仍对此算法不甚了解。网上大部分相关解析太过精简，萌新“初来乍看”不免云里雾里，故今日详细的将此算法叙述一番，希望对有需要的朋友有所帮助。至于博弈的相关概念网上资料很多，而且很详细，这里便不在赘余。

首先，我简单的介绍一下博弈树，这里由一个经典的例子引入：
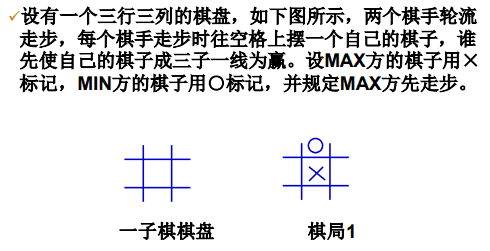
【人工智能】Alpha-Beta剪枝算法
所以可得：

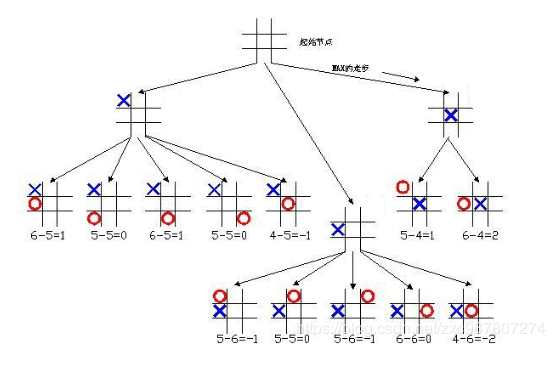
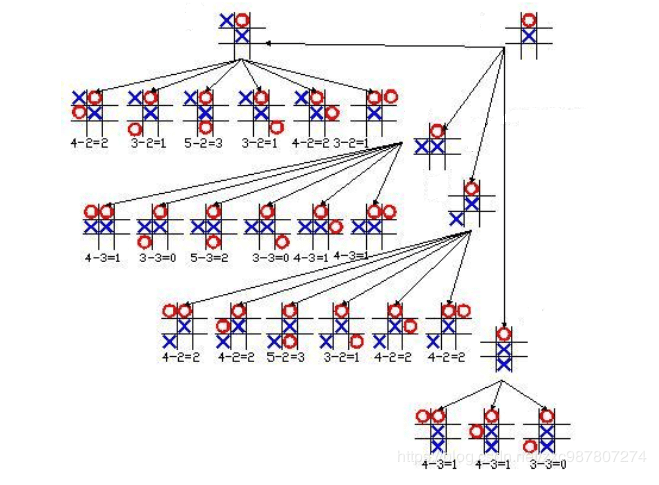
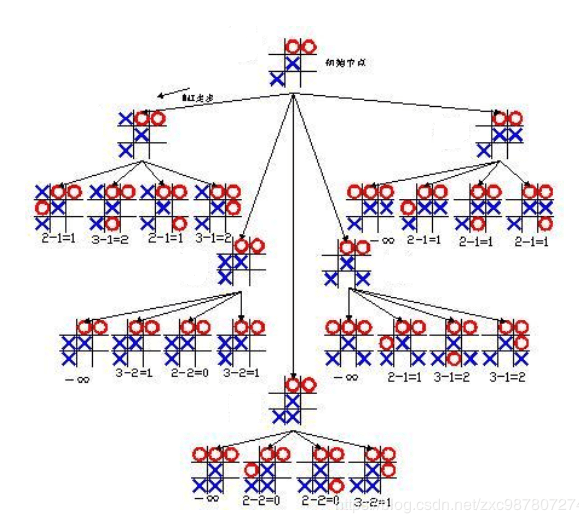
上图只计算了其中一部分，便可知完整博弈树的庞大复杂，为便于理解与计算，我们假设其完整的树如下图所示：

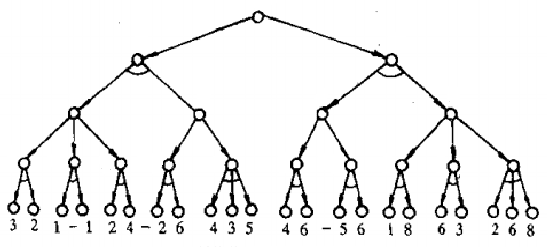
现在求此树的每层的值，需得保证己方获得的e（P）值最大，而对方的获得的e（P）值最校
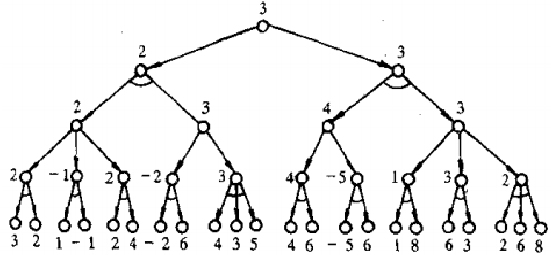
【人工智能】Alpha-Beta剪枝算法
即可求出最佳走法：

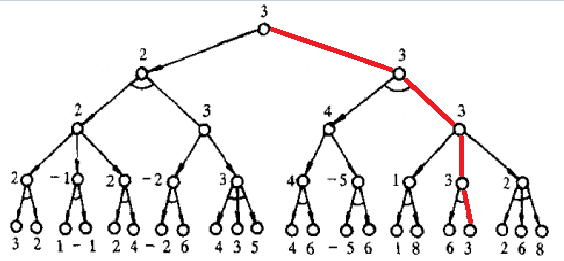
以上便是博弈树，在这里我们就会发现一个问题，要把树中所有枝叶上的值求出来，计算量未免太大，有没有更好的办法呢？这里，我们引出了Alpha-Beta剪枝算法。下面我将以图示的办法展现其过程：
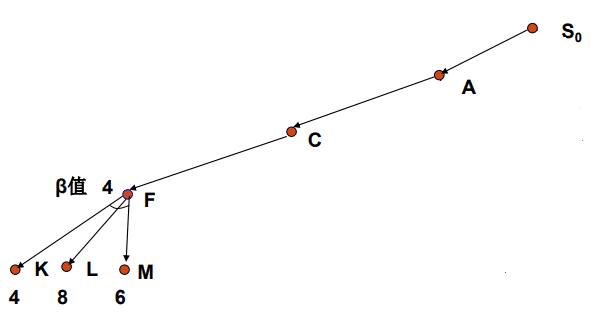
1.下图所示是一个只求出了三个估价值的四层博弈树。
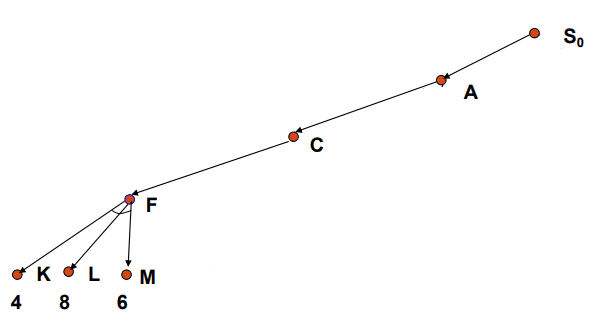
【人工智能】Alpha-Beta剪枝算法
2.我们可求出F点的估价值是4。

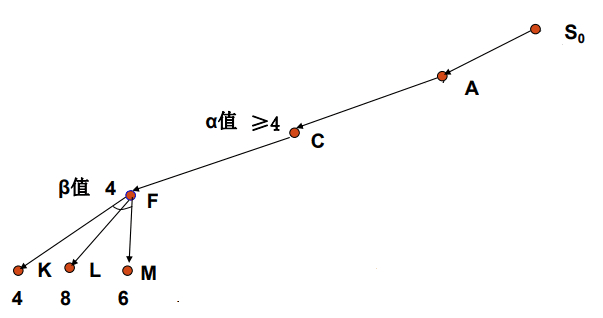
3.我们可知C点的估价值必定要大于等于4。

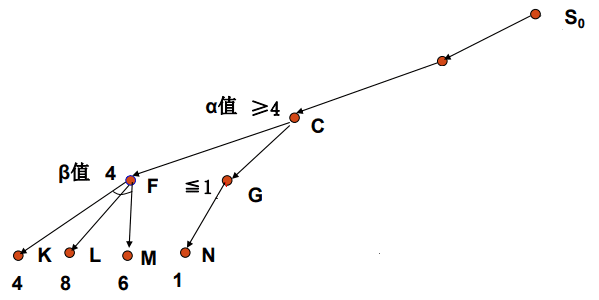
4.我们接着求N点的值，且可知G点的值必定要小于等于1。

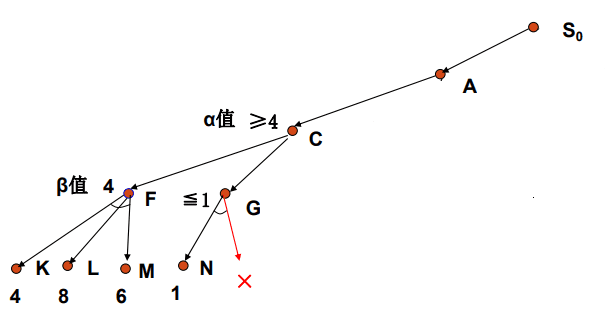
5.由于C点的值必然大于等于4，且G点的值已经小于等于1，故G点的另一条树枝的值不用计算，因为算出来也用不上。

【人工智能】Alpha-Beta剪枝算法
6.下面同理，得A的值必小于等于4，且D的值已经大于等于5，故D点的另一条树枝的值也不用计算。

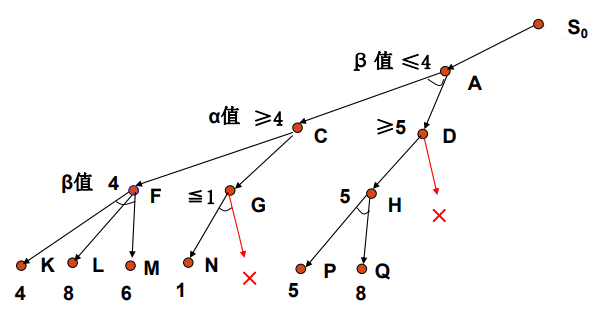
7.同理将剩余节点也如此处理。

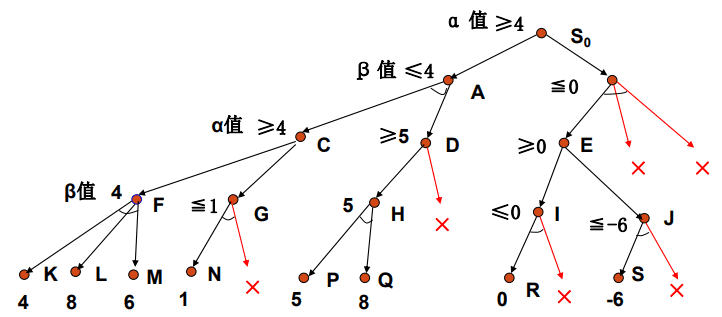
以上便是Alpha-Beta剪枝算法。
下面附上其Java语言实现方式（代码源自GitHub）：`

  private static MinimaxResult max(byte[][] chessBoard, int depth, int alpha, int beta, byte chessColor, int difficulty) {
    if (depth == 0) {
      return new MinimaxResult(evaluate(chessBoard, difficulty), null);
    }

    List<Move> legalMovesMe = Rule.getLegalMoves(chessBoard, chessColor);
    if (legalMovesMe.size() == 0) {
      if (Rule.getLegalMoves(chessBoard, (byte)-chessColor).size() == 0) {
        return new MinimaxResult(evaluate(chessBoard, difficulty), null);
      }
      return min(chessBoard, depth, alpha, beta, (byte)-chessColor, difficulty);
    }

    byte[][] tmp = new byte[8][8];
    Util.copyBinaryArray(chessBoard, tmp);
    int best = Integer.MIN_VALUE;
    Move move = null;

    for (int i = 0; i < legalMovesMe.size(); i++) {
      alpha = Math.max(best, alpha);
      if(alpha >= beta){
        break;
      }
      Rule.move(chessBoard, legalMovesMe.get(i), chessColor);
      int value = min(chessBoard, depth - 1, Math.max(best, alpha), beta, (byte)-chessColor, difficulty).mark;
      if (value > best) {
        best = value;
        move = legalMovesMe.get(i);
      }
      Util.copyBinaryArray(tmp, chessBoard);
    }
    return new MinimaxResult(best, move);
  }

  private static MinimaxResult min(byte[][] chessBoard, int depth, int alpha, int beta, byte chessColor, int difficulty) {
    if (depth == 0) {
      return new MinimaxResult(evaluate(chessBoard, difficulty), null);
    }

    List<Move> legalMovesMe = Rule.getLegalMoves(chessBoard, chessColor);
    if (legalMovesMe.size() == 0) {
      if (Rule.getLegalMoves(chessBoard, (byte)-chessColor).size() == 0) {
        return new MinimaxResult(evaluate(chessBoard, difficulty), null);
      }
      return max(chessBoard, depth, alpha, beta, (byte)-chessColor, difficulty);
    }

    byte[][] tmp = new byte[8][8];
    Util.copyBinaryArray(chessBoard, tmp);
    int best = Integer.MAX_VALUE;
    Move move = null;

    for (int i = 0; i < legalMovesMe.size(); i++) {
      beta = Math.min(best, beta);
      if(alpha >= beta){
        break;
      }
      Rule.move(chessBoard, legalMovesMe.get(i), chessColor);
      int value = max(chessBoard, depth - 1, alpha, Math.min(best, beta), (byte)-chessColor, difficulty).mark;
      if (value < best) {
        best = value;
        move = legalMovesMe.get(i);
      }
      Util.copyBinaryArray(tmp, chessBoard);
    }
    return new MinimaxResult(best, move);
  }

注明：本文章仅供学习参考之用，代码选自一款棋类博弈游戏。作者水平有限，不免有错漏之处，如有问题或建议，可留言告之。

路由器

电脑

手机

网络

【人工智能】Alpha-Beta剪枝算法

推荐阅读