UG9.0使用表达式集锦

UG9.0使用表达式集锦

表达式是通过三角函数数值来创建图形的一种方法，是属于特殊零件图形的构建，下面就以UG9.0软件为蓝本，对其表达式界面进行解说及应用技巧。

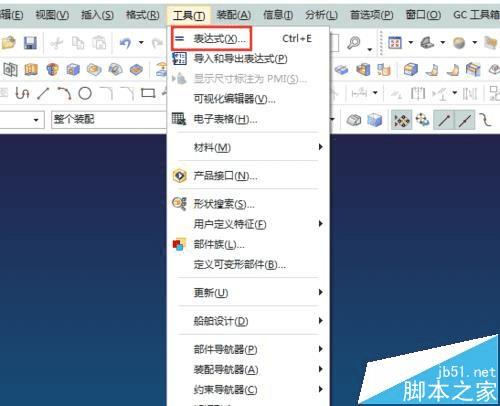
1、表达式输入：工具----表达式；快捷键是（ctrl+e)

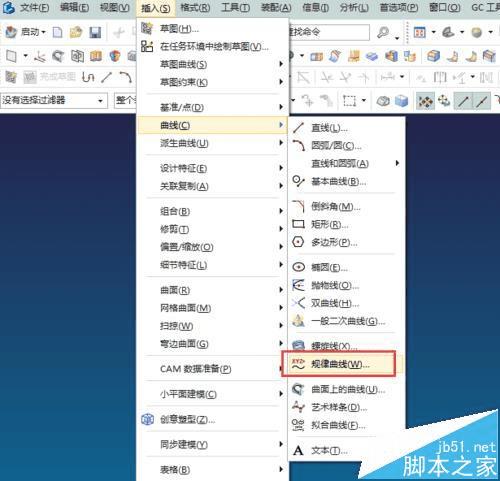
2、执行：插入----曲线----规律曲线----根据方程。如果没有“规律曲线”命令，用：帮助----命令查找器；查找。

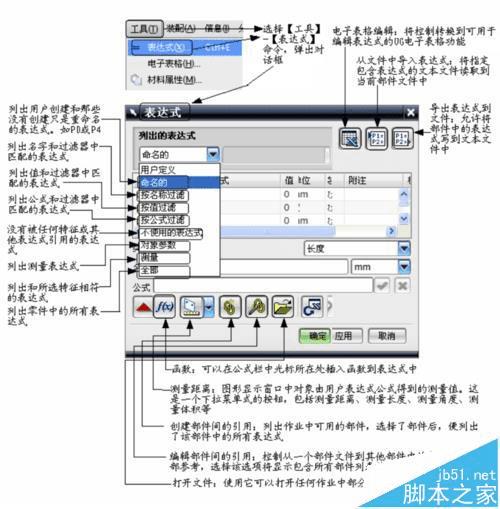
3、“表达式”对话框如下：

4、将方程转换为参数方程时注意：将方程转化为参数方程时，一定要将其转换为以变量t为参数的方程，在 UG中，t的变化范围一定是从0到1。

5、规律曲线命令如下：

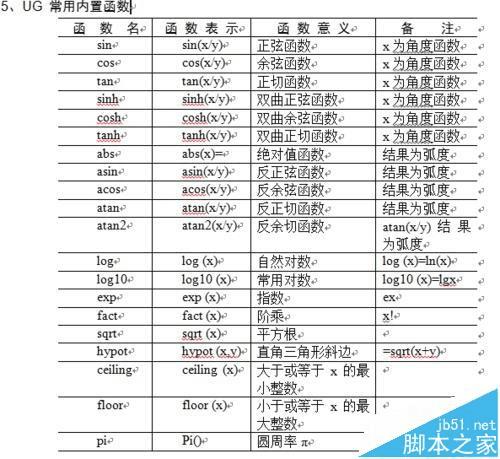
6、UG 常用内置函数

7、在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线：

1）极坐标（或柱坐标r,θ,z）与直角坐标系(x,y,z)的转换关系：

x=r*cos(θ)；y=r*sin(θ)；z=z

2）球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系：

x=rsinθcosφ；y=rsinθsinφ；z=rcosθ

在UG表达式中输入的theta=θ；phi=φ；r=rho

注：所有UG表达式中，必须先在名称栏输入t，公式栏输入0，类型为恒定的，即无单位。t是UG自带的系统变量，其取值为0~1之间的连续的数

8、直线

直线的数学方程为y-y0=tan(θ)*(x-x0)，若直线经过点（10,20），倾角θ为30°，长度L为40，即UG表达式为：

theta=30

L=40

xt=10+L*cos(theta)*t

yt=20+L*sin(theta)*t

zt=0

效果如图1

9、圆和圆弧

圆的数学方程为(x-x0)^2+(y-y0)^2=r^2，若圆心坐标为（50,40），半径r为30，即UG表达式为：

r=30

theta=t*360

xt=50+r*cos(theta)

yt=40+r*sin(theta)

zt=0

效果如图2

10、椭圆和椭圆弧

椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1，若椭圆中心坐标为（50,40），长半轴a为30（在X轴上），短半轴b为20，即UG表达式为：

a=30

b=20

theta=t*360

xt=50+a*cos(theta)

yt=40+b*sin(theta)

zt=0

效果如图3

11、双曲线

双曲线的数学方程为x2/a2-y2/b2=1，若中心坐标为（0,0），实长半轴a为4（在x轴上），虚半轴b为3，y的取值范围为-5~+5内的一段，即UG表达式为：

a=4

b=3

yt=10*t-5

xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)

zt=0

做出一半后进行镜像复制，效果如图4

12、抛物线

抛物线I的数学方程为y2=2px，若抛物线的顶点为（30,20）焦点到准线的距离p=8，y的取值范围为-25~+25，即UG表达式为：

p=8

yt=50*t-25+20

xt=(yt-20)^2/(2*p)+30

zt=0

效果如图5-1

抛物线II数学参数方程：x=3px2，y=3px（其中t为参数）。UG表达式为：

p=8

tt=t*4-2

xt=2*p*tt^2

yt=2*p*tt

zt=0

效果如图5-2