人工智能数学之信息论
信息论
信息论(Information Theory)是概率数理统计分支,我们主要看信息论在人工智能中的应用,所以目前只关注相关的信息。例如基于信息增益的决策树,最大熵模型, 特征工程中特征选取时用到的互信息,模型损失函数的交叉熵(cross-entropy)。信息论中log默认以2为底。
基础
1.熵
直观来说熵就是表示事情不确定性的因素度量,熵越大不确定性就越大,而不确定性越大,带来的信息则越多,所以在熵越高,带来的信息越多,不确定性越强。但是确定的东西,带来的不确定性很小,信息也很少,所以熵很低。熵=不确定性=信息量。他们三个成正比例。例如太阳东升西落,熵就为0。一枚质地均匀的硬币,正反面的出现,熵就为1。
公式
设X为离散随机变量,概率分布:
P ( X = xi ) = pi, i = 1,2,3,…,n
则随机变量X的熵为:
H(p) = -∑ pi * log pi
由上式可以得出,太阳东升西落、硬币正反面的熵运算。
2.条件熵
信息增益理解之前我们要理解一下条件熵,信息增益字面理解,信息增加后对最后的目标结果有多大的益处。也就是说通过选择合适的X特征作为判断信息,让Y的不确定性减少的程度越大,则选择出的X越好。而条件熵H(Y|X)表达就是给定X后,Y的不确定性是多少。
H ( Y | X ) = -∑ pi * H ( Y | X = xi )
这里 pi = P( X = xi ) ,i = 1,2,…,n
熵和条件熵中的概率如果通过估计得到,例如极大似然估计,则熵和条件熵将会,变名字经验熵和经验条件熵。
交叉熵损失函数
交叉熵被设置为模型的损失函数,表示的两个概率分布的相似程度,交叉熵越小代表预测的越接近真实。q(x)代表的是预测概率,p(x)代表的是真实概率。
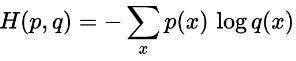
二分类问题交叉熵公式
L=-[ylog y^+(1-y)log (1-y^)]
y^代表预测的正例概率。y代表真实标签。模型可以是逻辑回归或者是神经网络,输出值映射成概率值需要sigmoid函数。所以如果二分类的标签值是0和1。则公式可以写成。
L=-log y^,y=1时,L值和预测值之间的图像
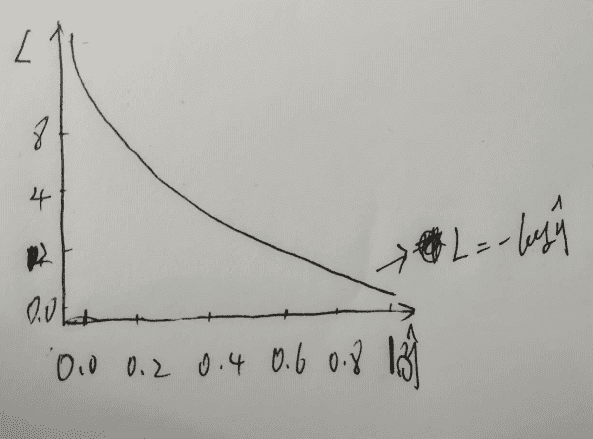
从图上我们可以看出,当预测值接近1,也就是接近真实值的时候,L交叉熵损失函数值越接近于0。这样我们可以直观的看出,交叉熵损失函数是如何表征了预测值到真实值之间的差距。
信息增益
信息增益直观来说就是当给了你一条信息X,这条信息对你理解另一条信息Y有没有帮助,如果有帮助,则会使你对信息Y的理解加深,不理解的信息减少。则信息增益就等于Y的熵减给定X后Y的熵。公式如下:
IG(Y|X) = H(Y)-H(Y|X)
信息增益作为决策树模型中的核心算法,是决策树模型中非叶子节点选择特征的重要评判标准,简单说一下决策树,决策树模型作为基于实例的模型,主要是叶节点(目标值或者目标类别),非叶节点是用于判断实例的特征属性。之后将依据信息论详细介绍决策树模型。
信息增益率
互信息(Mutual Information)
概率中两个随机变量的互信息是描述两个变量之间依赖性的度量。它也决定着两个变量的联合概率密度P(XY)与各自边际概率
P(X)和P(Y)乘积的相似程度。我们可以从概率学的知识了解到,如果X和Y之间相互独立,P(X)P(Y) = P(XY)。和相关系数不同,它不仅能获得线性关系,还可以获得非线性关系。互信息公式如下:
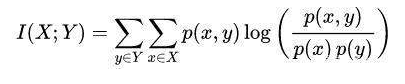
下图为连续型随机变量互信息的公式:
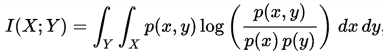
p(x,y) 当前是 X 和 Y 的联合概率密度函数,而p(x)和p(y)分别是 X 和 Y 的边缘概率密度函数。
直观来说,互信息就是度量当已知一个信息,会对另一个信息的不确定性减少的程度,如果XY相互独立,则X不会减少Y的不确定性,互信息为0。所以互信息是非负的。