怎么样解决一道正方体六个面上的四个角点整数之和相等”的问题？
怎么样解决一道正方体六个面上的四个角点整数之和相等”的问题？
题目:
请将8个给定的正整数（如1，2，3，4，5，6，7，8）分别放在一个正方体的8个角的顶点上，以实现如下要求（如果可能）：正方体六个面上的四个角点整数之和相等？输出结果如：A1=1,A2=2...
求解如下
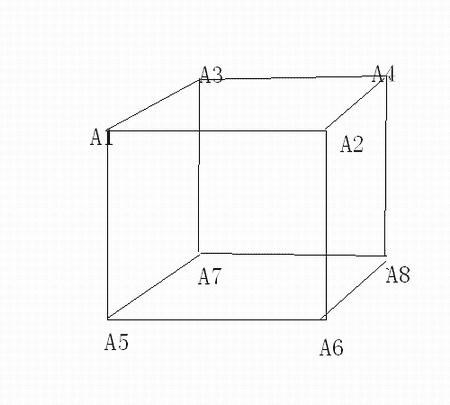
算法思路
根据题境，我们先做如下设定和术语说明，以便于后面的讨论：
１、正整数以１，２，３，４，。。。８表示，以便进行分析；
２、正方体顶点标示如上所示；
３、每一个面的四个顶点数总和，我们称为该面的面积；
４、每一条边的两个顶点数和，我们称为该边的长度；
通过分析,可以得到如下断言为真（采用上面设定及术语）：
１、每个面的面积相等，且每个面的面积为３６／２，即１８；
２、正方体的对边相等；
３、整数１和（２，３）不在同一边，整数７和８不在同一边；
根据所得断言，可以得到如下求导公式和约束：
A1=1;
A4=18-A1-A2-A3=17-A2-A3;
A6=18-A1-A2-A5=17-A2-A5;
A7=18-A1-A3-A5=17-A3-A5;
A8=A1+A2-A7=2*A1+A2+A3+A5-18=A2+A3+A5-16;
A2，A3，A5为可变量，但是A2，A3不等于２，３
程序实现
通过以上算法分析，可用程序实现如下（Java实现）：
packageqinysong.arithmetic;
publicclassCubeProblem{
publicstaticvoidmain(String[]args){
System.out.println("CubeProblembegin........");
searchPeekNumber();
System.out.println("CubeProblemend........");
}
publicstaticvoidprintPeekNumbers(int[]peeks){
System.out.println("thepeeknumber:A1="+peeks[0]+";A2="+peeks[1]
+";A3="+peeks[2]+";A4="+peeks[3]
+";A5="+peeks[4]+";A6="+peeks[5]
+";A7="+peeks[6]+";A8="+peeks[7]);
}
//核心函数，探寻各个顶点的数值
publicstaticvoidsearchPeekNumber(){
int[]peeks=newint[8];
intpeekNumber=0;
for(inti=4;i<=8;i++){
peeks[0]=1;
peeks[1]=i;
for(intj=4;j<=8;j++){
if(hasUsed(2,j,peeks))continue;
peeks[2]=j;
peekNumber=getPeekNumber(3,peeks);
peeks[3]=peekNumber;
for(intk=2;k<=8;k++){
if(hasUsed(4,k,peeks))continue;
peeks[4]=k;
peekNumber=getPeekNumber(5,peeks);
if(hasUsed(5,peekNumber,peeks))continue;
peeks[5]=peekNumber;
peekNumber=getPeekNumber(6,peeks);
if(hasUsed(6,peekNumber,peeks))continue;
peeks[6]=peekNumber;
peekNumber=getPeekNumber(7,peeks);
if(hasUsed(7,peekNumber,peeks))continue;
peeks[7]=peekNumber;
printPeekNumbers(peeks);
}
}
}
}
/**
*判断获取的顶点值是否在之前的顶点使用过
*@paramindexint将要赋值的顶点索引
*@parampeekNumberint获取的顶点值
*@returnboolean是否在之前的顶点使用过
*/
publicstaticbooleanhasUsed(intindex,intpeekNumber,int[]peeks){
if(peekNumber<=0)returntrue;
for(inti=0;i<index;i++){
if(peeks[i]==peekNumber){
returntrue;
}
}
returnfalse;
}
/**
*取得某一顶点的数值
*根据推导公式：
*A4=18-A1-A2-A3；A6=18-A1-A2-A5；A7=18-A1-A3-A5；A8=2*A1+A2+A3+A5-18；
*这里取A1=1
*@parampeekint顶点标号
*@returnint顶点数值
*/
publicstaticintgetPeekNumber(intpeek,int[]peeks){
switch(peek){
case0:
return1;
case3:
return17-peeks[1]-peeks[2];
case5:
return17-peeks[1]-peeks[4];
case6:
return17-peeks[2]-peeks[4];
case7:
returnpeeks[1]+peeks[2]+peeks[4]-16;
default:
return0;
}
}
}
publicclassCubeProblem{
publicstaticvoidmain(String[]args){
System.out.println("CubeProblembegin........");
searchPeekNumber();
System.out.println("CubeProblemend........");
}
publicstaticvoidprintPeekNumbers(int[]peeks){
System.out.println("thepeeknumber:A1="+peeks[0]+";A2="+peeks[1]
+";A3="+peeks[2]+";A4="+peeks[3]
+";A5="+peeks[4]+";A6="+peeks[5]
+";A7="+peeks[6]+";A8="+peeks[7]);
}
//核心函数，探寻各个顶点的数值
publicstaticvoidsearchPeekNumber(){
int[]peeks=newint[8];
intpeekNumber=0;
for(inti=4;i<=8;i++){
peeks[0]=1;
peeks[1]=i;
for(intj=4;j<=8;j++){
if(hasUsed(2,j,peeks))continue;
peeks[2]=j;
peekNumber=getPeekNumber(3,peeks);
peeks[3]=peekNumber;
for(intk=2;k<=8;k++){
if(hasUsed(4,k,peeks))continue;
peeks[4]=k;
peekNumber=getPeekNumber(5,peeks);
if(hasUsed(5,peekNumber,peeks))continue;
peeks[5]=peekNumber;
peekNumber=getPeekNumber(6,peeks);
if(hasUsed(6,peekNumber,peeks))continue;
peeks[6]=peekNumber;
peekNumber=getPeekNumber(7,peeks);
if(hasUsed(7,peekNumber,peeks))continue;
peeks[7]=peekNumber;
printPeekNumbers(peeks);
}
}
}
}
/**
*判断获取的顶点值是否在之前的顶点使用过
*@paramindexint将要赋值的顶点索引
*@parampeekNumberint获取的顶点值
*@returnboolean是否在之前的顶点使用过
*/
publicstaticbooleanhasUsed(intindex,intpeekNumber,int[]peeks){
if(peekNumber<=0)returntrue;
for(inti=0;i<index;i++){
if(peeks[i]==peekNumber){
returntrue;
}
}
returnfalse;
}
/**
*取得某一顶点的数值
*根据推导公式：
*A4=18-A1-A2-A3；A6=18-A1-A2-A5；A7=18-A1-A3-A5；A8=2*A1+A2+A3+A5-18；
*这里取A1=1
*@parampeekint顶点标号
*@returnint顶点数值
*/
publicstaticintgetPeekNumber(intpeek,int[]peeks){
switch(peek){
case0:
return1;
case3:
return17-peeks[1]-peeks[2];
case5:
return17-peeks[1]-peeks[4];
case6:
return17-peeks[2]-peeks[4];
case7:
returnpeeks[1]+peeks[2]+peeks[4]-16;
default:
return0;
}
}
}
执行结果如下
CubeProblembegin........thepeeknumber:A1=1;A2=4;A3=6;A4=7;A5=8;A6=5;A7=3;A8=2thepeeknumber:A1=1;A2=4;A3=7;A4=6;A5=8;A6=5;A7=2;A8=3thepeeknumber:A1=1;A2=4;A3=8;A4=5;A5=6;A6=7;A7=3;A8=2thepeeknumber:A1=1;A2=4;A3=8;A4=5;A5=7;A6=6;A7=2;A8=3thepeeknumber:A1=1;A2=6;A3=4;A4=7;A5=8;A6=3;A7=5;A8=2thepeeknumber:A1=1;A2=6;A3=7;A4=4;A5=8;A6=3;A7=2;A8=5thepeeknumber:A1=1;A2=6;A3=8;A4=3;A5=4;A6=7;A7=5;A8=2thepeeknumber:A1=1;A2=6;A3=8;A4=3;A5=7;A6=4;A7=2;A8=5thepeeknumber:A1=1;A2=7;A3=4;A4=6;A5=8;A6=2;A7=5;A8=3thepeeknumber:A1=1;A2=7;A3=6;A4=4;A5=8;A6=2;A7=3;A8=5thepeeknumber:A1=1;A2=7;A3=8;A4=2;A5=4;A6=6;A7=5;A8=3thepeeknumber:A1=1;A2=7;A3=8;A4=2;A5=6;A6=4;A7=3;A8=5thepeeknumber:A1=1;A2=8;A3=4;A4=5;A5=6;A6=3;A7=7;A8=2thepeeknumber:A1=1;A2=8;A3=4;A4=5;A5=7;A6=2;A7=6;A8=3thepeeknumber:A1=1;A2=8;A3=6;A4=3;A5=4;A6=5;A7=7;A8=2thepeeknumber:A1=1;A2=8;A3=6;A4=3;A5=7;A6=2;A7=4;A8=5thepeeknumber:A1=1;A2=8;A3=7;A4=2;A5=4;A6=5;A7=6;A8=3thepeeknumber:A1=1;A2=8;A3=7;A4=2;A5=6;A6=3;A7=4;A8=5CubeProblemend........
算法特性
因为该算法是根据分析问题的数学模型，找到推导公式及数值约束，然后直接推导答案，而不是采用通过遍历每一种可能性进行判断，所以效率非常好