区块链01.RSA
0.数字货币的本质问题
账户数字化:唯一性问题
签名数字化:身份认证问题
记账去中心化:分布式数据完整性问题
1.密钥分发问题(对称密码)
1.1密钥问题:
密钥是用来加密文件的,文件和密钥如果通过同一渠道传出(eg.qq / wechat),假设文件因为不安全需要保护,则密钥在该渠道下也是不安全的。所以密钥形同虚设。
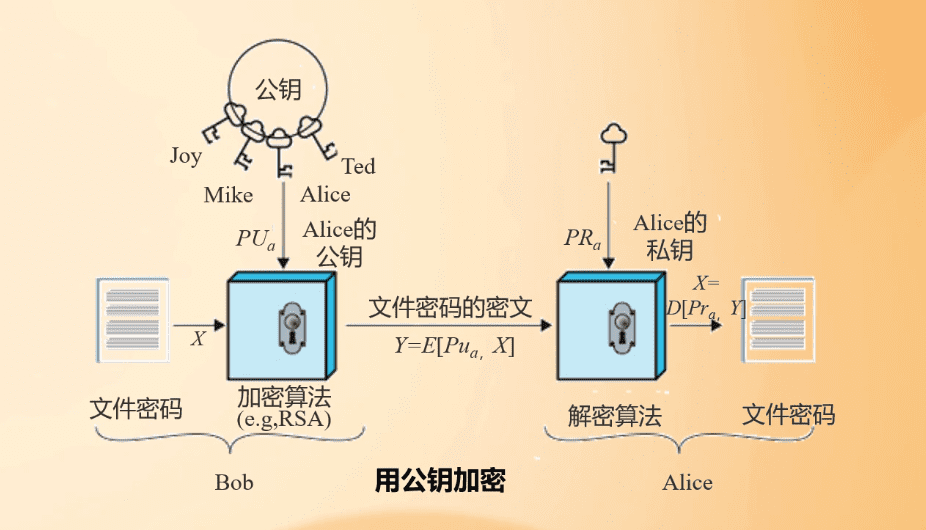
1.1解决办法:公钥密码
公钥密码的性质(非对称密码):
一个公钥对应一个私钥,他们都是密钥。
密钥对中,让大家都知道的是公钥,不告诉大家,只有自己知道的,是私钥。
如果用其中一个密钥加密数据,则只有对应的那个密钥才可以解密。
如果用其中一个密钥可以进行解密数据,则该数据必然是对应的那个密钥进行的加密。
2.身份认证问题
2.1解决方案
发给想验证我的人一份明文和一份我的密钥加密过的密文,如果对方用公钥解密密文后和我发送的名文相同说明我是我。
3.RSA的数学基础
3.1整除
if a整除b,记为 a|b,a是除数,b是被除数
若 c = k1a + k2b;e|a 则 e|b 且 e|c。
3.2最大公因子
a和b的最大公因子记为(a,b)或 gcd(a,b)
若 a = k*b + c 则(a,b) = (b,c)//0<=c&&c<b
3.3欧几里得算法(辗转相除法)
eg。求1997 和 615的最大公因子

3.4扩展欧几里得算法
k1a+k2b = (a, b) 可求
3.5互素
若 k1a+k2b =(a,b)= 1,则互素,
此时k1为a的乘法逆元
3.5欧拉函数
Φ(n):小于n大于0的数中与n互素的数的数量
n可以表示为所有素因子的乘积(p1.。。。ps),每次剔除n个数中某个素因子对应的非互素的数
4.RSA
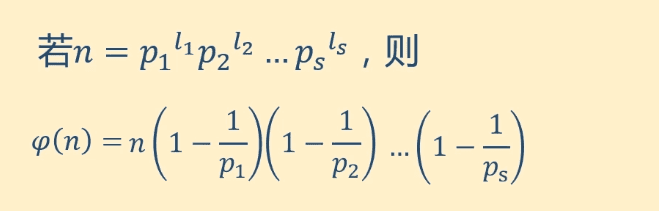
3.6欧拉定理
若(a,n) = 1,则(a^Φ(n))mod n = 1;
欧拉定理的推论

4.RSA
4.1思想:
攻击者根据公钥只要直到n的所有素因子就可以算出来密钥,所以让n只有两个素因子并且n很大则可以使攻击者无法用公钥计算出
4.2RSA原理
